streamalism.org

1. Inleiding

Pathfinding-algoritmen zijn technieken om door kaarten te navigeren, waardoor we een route kunnen vinden tussen twee verschillende punten. Verschillende algoritmen hebben verschillende voor- en nadelen, vaak in termen van de efficiëntie van het algoritme en de efficiëntie van de route die het genereert.

2. Wat is een Pathfinding-algoritme?

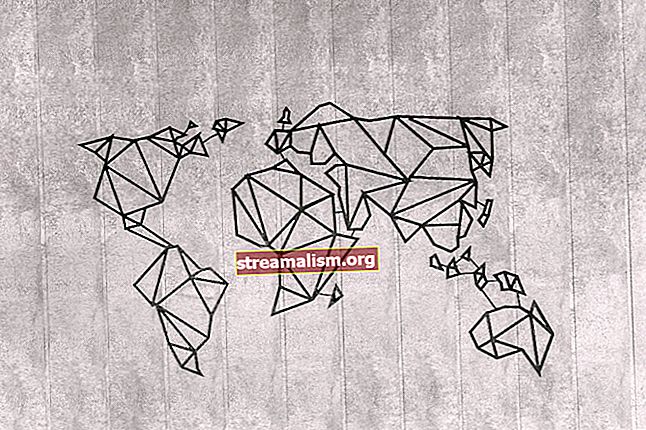
Een Pathfinding Algorithm is een techniek om een ​​grafiek - bestaande uit knooppunten en randen - om te zetten in een route door de grafiek. Deze grafiek kan van alles zijn dat moet worden doorlopen. Voor dit artikel gaan we proberen een deel van het Londense metrosysteem te doorkruisen:

("London Underground Overground DLR Crossrail map" door sameboat is gelicentieerd onder CC BY-SA 4.0)

Dit heeft veel interessante componenten:

• We hebben al dan niet een directe route tussen onze start- en eindpunten. We kunnen bijvoorbeeld rechtstreeks van "Earl's Court" naar "Monument" gaan, maar niet naar "Angel".
• Elke stap heeft zijn eigen kosten. In ons geval is dit de afstand tussen stations.
• Elke halte is slechts verbonden met een kleine subset van de andere haltes. Zo is "Regent's Park" alleen rechtstreeks verbonden met "Baker Street" en "Oxford Circus".

Alle pathfinding-algoritmen nemen als invoer een verzameling van alle knooppunten - stations in ons geval - en verbindingen daartussen, en ook de gewenste start- en eindpunten. De uitvoer is meestal de set knooppunten die ons van begin tot eind brengen, in de volgorde die we nodig hebben.

3. Wat is A *?

A * is een specifiek algoritme voor het vinden van paden, voor het eerst gepubliceerd in 1968 door Peter Hart, Nils Nilsson en Bertram Raphael. Het wordt algemeen beschouwd als het beste algoritme om te gebruiken wanneer er geen mogelijkheid is om de routes vooraf te berekenen en er geen beperkingen zijn aan het geheugengebruik..

Zowel geheugen als prestaties kunnen complex zijn O (b ^ d) in het ergste geval, dus hoewel het altijd de meest efficiënte route zal uitwerken, is het niet altijd de meest efficiënte manier om dat te doen.

A * is eigenlijk een variatie op Dijkstra's algoritme, waar er aanvullende informatie wordt verstrekt om te helpen bij het selecteren van het volgende knooppunt dat moet worden gebruikt. Deze aanvullende informatie hoeft niet perfect te zijn - als we al perfecte informatie hebben, heeft het zoeken naar paden geen zin. Maar hoe beter het is, hoe beter het eindresultaat zal zijn.

4. Hoe werkt A *?

Het A * -algoritme werkt door iteratief te selecteren wat tot nu toe de beste route is, en te proberen te zien wat de beste volgende stap is.

Als we met dit algoritme werken, hebben we verschillende gegevens die we moeten bijhouden. De "open set" zijn alle knooppunten die we momenteel overwegen. Dit is niet elk knooppunt in het systeem, maar in plaats daarvan is het elk knooppunt waaruit we de volgende stap kunnen maken.

We houden ook de huidige beste score, de geschatte totale score en het huidige beste vorige knooppunt bij voor elk knooppunt in het systeem.

Als onderdeel hiervan moeten we twee verschillende scores kunnen berekenen. Een daarvan is de score om van het ene knooppunt naar het andere te gaan. De tweede is een heuristiek om een ​​schatting te geven van de kosten vanaf elk knooppunt naar de bestemming. Deze schatting hoeft niet nauwkeurig te zijn, maar een grotere nauwkeurigheid zal betere resultaten opleveren. De enige vereiste is dat beide scores consistent zijn met elkaar, dat wil zeggen dat ze in dezelfde eenheden zitten.

Helemaal aan het begin bestaat onze open set uit ons startknooppunt en we hebben helemaal geen informatie over andere knooppunten.

Bij elke iteratie zullen we:

• Selecteer het knooppunt uit onze open set met de laagste geschatte totale score
• Verwijder dit knooppunt uit de open set
• Voeg aan de open set alle knooppunten toe die we ervan kunnen bereiken

Wanneer we dit doen, werken we ook de nieuwe score uit van dit knooppunt naar elk nieuw knooppunt om te zien of het een verbetering is ten opzichte van wat we tot nu toe hebben, en als dat zo is, werken we bij wat we weten over dat knooppunt.

Dit herhaalt zich dan totdat het knooppunt in onze open set met de laagste geschatte totale score onze bestemming is, op welk punt we onze route hebben.

4.1. Uitgewerkt voorbeeld

Laten we bijvoorbeeld beginnen met "Marylebone" en proberen de weg naar "Bond Street" te vinden.

In het begin bestaat onze open set alleen uit "Marylebone". Dat betekent dat dit impliciet het knooppunt is waarvoor we de beste "geschatte totaalscore" hebben.

Onze volgende stops kunnen ofwel "Edgware Road" zijn, met een kostprijs van 0,4403 km, of "Baker Street", met een kostprijs van 0,4153 km. "Edgware Road" is echter in de verkeerde richting, dus onze heuristiek van hier naar de bestemming geeft een score van 1,4284 km, terwijl "Baker Street" een heuristische score van 1,0753 km heeft.

Dit betekent dat onze open set na deze iteratie uit twee inzendingen bestaat - “Edgware Road”, met een geschatte totale score van 1.8687 km, en “Baker Street”, met een geschatte totale score van 1.4906 km.

Onze tweede iteratie begint dan bij "Baker Street", aangezien deze de laagste geschatte totaalscore heeft. Vanaf hier kunnen onze volgende haltes ofwel "Marylebone", "St. John's Wood ”,“ Great Portland Street ”, Regent's Park” of “Bond Street”.

We zullen deze niet allemaal behandelen, maar laten we "Marylebone" als interessant voorbeeld nemen. De kosten om er te komen zijn weer 0,4153 km, maar dit betekent dat de totale kosten nu 0,8306 km bedragen. Bovendien geeft de heuristiek van hier naar de bestemming een score van 1,323 km.

Dit betekent dat de geschatte totale score 2,1536 km zou zijn, dat is erger dan de vorige score voor dit knooppunt. Dit is logisch, want we hebben extra werk moeten doen om in dit geval nergens te komen. Dit betekent dat we dit niet als een haalbare route zullen beschouwen. Als zodanig worden de details voor "Marylebone" niet bijgewerkt en wordt het niet opnieuw toegevoegd aan de open set.

5. Java-implementatie

Nu we hebben besproken hoe dit werkt, gaan we het daadwerkelijk implementeren. We gaan een generieke oplossing bouwen en vervolgens de code implementeren die nodig is om te werken voor de Londense metro. We kunnen het dan gebruiken voor andere scenario's door alleen die specifieke onderdelen te implementeren.

5.1. Vertegenwoordigt de grafiek

Ten eerste moeten we in staat zijn om onze grafiek weer te geven die we willen doorlopen. Dit bestaat uit twee klassen: de afzonderlijke knooppunten en vervolgens de grafiek als geheel.

We vertegenwoordigen onze individuele knooppunten met een interface genaamd GraphNode:

openbare interface GraphNode {String getId (); }

Elk van onze knooppunten moet een ID hebben. Al het andere is specifiek voor deze specifieke grafiek en is niet nodig voor de algemene oplossing. Deze klassen zijn eenvoudige Java Beans zonder speciale logica.

Onze algemene grafiek wordt dan weergegeven door een klasse die eenvoudigweg wordt genoemd Grafiek:

openbare klasse Graph {private final Set nodes; privé definitieve kaart verbindingen; public T getNode (String id) {return nodes.stream () .filter (node ​​-> node.getId (). equals (id)) .findFirst () .orElseThrow (() -> new IllegalArgumentException ("Geen knooppunt gevonden met ID KAART")); } public Set getConnections (T-node) {return connections.get (node.getId ()). stream () .map (this :: getNode) .collect (Collectors.toSet ()); }}

Dit slaat alle knooppunten in onze grafiek op en weet welke knooppunten met welke verbinding maken. We kunnen dan elk knooppunt op ID krijgen, of alle knooppunten die met een bepaald knooppunt zijn verbonden.

Op dit punt zijn we in staat om elke gewenste vorm van grafiek weer te geven, met een willekeurig aantal randen tussen een willekeurig aantal knooppunten.

5.2. Stappen op onze route

Het volgende dat we nodig hebben, is ons mechanisme om routes door de grafiek te vinden.

Het eerste deel hiervan is een manier om een ​​score te genereren tussen twee willekeurige knooppunten. We zullen het Scorer interface voor zowel de score naar het volgende knooppunt als de schatting naar de bestemming:

publieke interface Scorer {double computeCost (T from, T to); }

Gegeven een begin- en een eindknooppunt, krijgen we een score voor het reizen tussen beide.

We hebben ook een omhulsel nodig rond onze knooppunten dat wat extra informatie bevat. In plaats van een GraphNode, dit is een RouteNode - omdat het een knooppunt is in onze berekende route in plaats van een in de hele grafiek:

klasse RouteNode implementeert vergelijkbare {privé laatste T-stroom; privé T vorige; privé dubbele routeScore; privé dubbele geschatte score; RouteNode (T huidige) {dit (huidig, null, Double.POSITIVE_INFINITY, Double.POSITIVE_INFINITY); } RouteNode (T huidige, T vorige, dubbele routeScore, dubbele geschatte score) {this.current = huidig; this.previous = vorige; this.routeScore = routeScore; this.estimatedScore = geschatte score; }}

Net als bij GraphNode, dit zijn eenvoudige Java-bonen die worden gebruikt om de huidige status van elk knooppunt op te slaan voor de huidige routeberekening. We hebben dit een eenvoudige constructor gegeven voor het algemene geval, wanneer we voor het eerst een knooppunt bezoeken en er nog geen aanvullende informatie over hebben.

Deze moeten ook zijn Vergelijkbaar zodat we ze kunnen ordenen op basis van de geschatte score als onderdeel van het algoritme. Dit betekent de toevoeging van een vergelijk met() methode om te voldoen aan de vereisten van de Vergelijkbaar koppel:

@Override public int CompareTo (RouteNode other) {if (this.estimatedScore> other.estimatedScore) {return 1; } else if (this.estimatedScore <other.estimatedScore) {return -1; } else {return 0; }}

5.3. Onze route vinden

Nu zijn we in staat om onze routes in onze grafiek daadwerkelijk te genereren. Dit wordt een klas genaamd RouteFinder:

openbare klasse RouteFinder {privé definitieve grafiekgrafiek; privé-eindscorer nextNodeScorer; privé eindscorer targetScorer; openbare lijst findRoute (T from, T to) {throw new IllegalStateException ("Geen route gevonden"); }}

We hebben de grafiek waar we de routes over vinden, en onze twee scorers - een voor de exacte score voor het volgende knooppunt, en een voor de geschatte score naar onze bestemming. We hebben ook een methode die een begin- en eindknooppunt gebruikt en de beste route tussen de twee berekent.

Deze methode moet ons A * -algoritme zijn. Al de rest van onze code past in deze methode.

We beginnen met een aantal basisinstellingen - onze "open set" knooppunten die we als de volgende stap kunnen beschouwen, en een kaart van elk knooppunt dat we tot nu toe hebben bezocht en wat we ervan weten:

Wachtrij openSet = nieuwe PriorityQueue (); Kaart allNodes = nieuwe HashMap (); RouteNode start = nieuwe RouteNode (van, null, 0d, targetScorer.computeCost (van, naar)); openSet.add (start); allNodes.put (van, start);

Onze open set heeft in eerste instantie een enkel knooppunt - ons startpunt. Er is hiervoor geen vorig knooppunt, er is een score van 0 om daar te komen en we hebben een schatting van hoe ver het van onze bestemming is.

Het gebruik van een Prioriteits-rij voor de open set betekent dat we er automatisch de beste inzending van krijgen, op basis van onze vergelijk met() methode van vroeger.

Nu herhalen we totdat we geen knooppunten meer hebben om naar te kijken, of het best beschikbare knooppunt onze bestemming is:

while (! openSet.isEmpty ()) {RouteNode next = openSet.poll (); if (next.getCurrent (). equals (to)) {List route = new ArrayList (); RouteNode huidige = volgende; doe {route.add (0, current.getCurrent ()); current = allNodes.get (current.getPrevious ()); } while (current! = null); terugweg; } // ...

Als we onze bestemming hebben gevonden, kunnen we onze route opbouwen door herhaaldelijk naar het vorige knooppunt te kijken totdat we ons startpunt bereiken.

Vervolgens, als we onze bestemming niet hebben bereikt, kunnen we uitzoeken wat we nu moeten doen:

 graph.getConnections (next.getCurrent ()). forEach (verbinding -> {RouteNode nextNode = allNodes.getOrDefault (verbinding, nieuwe RouteNode (verbinding)); allNodes.put (verbinding, nextNode); dubbele newScore = next.getRouteScore () + nextNodeScorer.computeCost (next.getCurrent (), verbinding); if (newScore <nextNode.getRouteScore ()) {nextNode.setPrevious (next.getCurrent ()); nextNode.setRouteScore (newScore); nextNode.setEstimatedScore (newScore + targetScorer .computeCost (verbinding, naar)); openSet.add (nextNode);}}); gooi nieuwe IllegalStateException ("Geen route gevonden"); }

Hier itereren we over de verbonden knooppunten uit onze grafiek. Voor elk van deze krijgen we de RouteNode die we ervoor hebben - zo nodig een nieuwe maken.

We berekenen vervolgens de nieuwe score voor dit knooppunt en kijken of het goedkoper is dan wat we tot nu toe hadden. Als dit het geval is, werken we het bij zodat het overeenkomt met deze nieuwe route en voegen we het toe aan de open set voor overweging de volgende keer.

Dit is het hele algoritme. We blijven dit herhalen totdat we ons doel bereiken of er niet komen.

5.4. Specifieke details voor de Londense metro

Wat we tot nu toe hebben, is een generieke A * pathfinder, maar het mist de details die we nodig hebben voor ons exacte gebruiksscenario. Dit betekent dat we een concrete implementatie van beide nodig hebben GraphNode en Scorer.

Onze knooppunten zijn stations in de metro en we zullen ze modelleren met de Station klasse:

public class Station implementeert GraphNode {private final String id; private laatste String naam; private laatste dubbele breedtegraad; private laatste dubbele lengtegraad; }

De naam is handig om de uitvoer te zien, en de lengte- en breedtegraad zijn voor onze score.

In dit scenario hebben we slechts één implementatie van Scorer. We gaan hiervoor de Haversine-formule gebruiken om de afstand in rechte lijn tussen twee paren breedte- / lengtegraad te berekenen:

openbare klasse HaversineScorer implementeert Scorer {@Override openbare dubbele computeCost (Station van, Station naar) {dubbele R = 6372,8; // Radius van de aarde, in kilometers dubbele dLat = Math.toRadians (to.getLatitude () - from.getLatitude ()); dubbele dLon = Math.toRadians (to.getLongitude () - from.getLongitude ()); double lat1 = Math.toRadians (from.getLatitude ()); dubbele lat2 = Math.toRadians (to.getLatitude ()); dubbel a = Math.pow (Math.sin (dLat / 2), 2) + Math.pow (Math.sin (dLon / 2), 2) * Math.cos (lat1) * Math.cos (lat2); dubbele c = 2 * Math.asin (Math.sqrt (a)); retourneer R * c; }}

We hebben nu bijna alles wat nodig is om paden tussen twee willekeurige stations te berekenen. Het enige dat ontbreekt, is de grafiek van de onderlinge verbindingen. Dit is beschikbaar in GitHub.

Laten we het gebruiken om een ​​route uit te stippelen. We genereren er een van Earl's Court tot Angel. Dit heeft een aantal verschillende opties om te reizen, op minimaal twee metrolijnen:

openbare ongeldige findRoute () {Lijst route = routeFinder.findRoute (underground.getNode ("74"), underground.getNode ("7")); System.out.println (route.stream (). Map (Station :: getName) .collect (Collectors.toList ())); }

Dit genereert een route van Earl's Court -> South Kensington -> Green Park -> Euston -> Angel.

De voor de hand liggende route die veel mensen zouden hebben genomen, zou waarschijnlijk Earl's Count -> Monument -> Angel zijn, omdat dat minder veranderingen heeft ondergaan. In plaats daarvan, dit is een beduidend directere weg ingeslagen, hoewel het meer veranderingen met zich meebracht.

6. Conclusie

In dit artikel hebben we gezien wat het A * -algoritme is, hoe het werkt en hoe we het in onze eigen projecten kunnen implementeren. Waarom zou u dit niet nemen en uitbreiden voor uw eigen gebruik?

Probeer het misschien uit te breiden om rekening te houden met de uitwisselingen tussen metrolijnen, en kijk hoe dat de geselecteerde routes beïnvloedt?

En nogmaals, de volledige code voor het artikel is beschikbaar op GitHub.