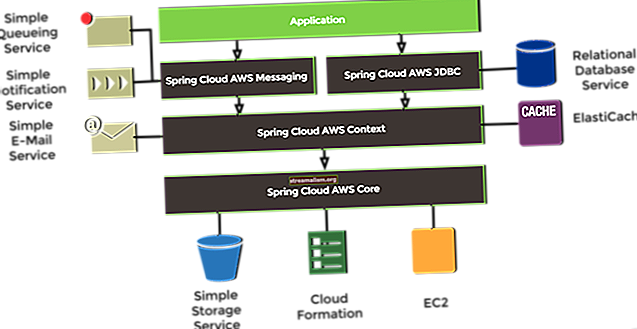
Een doolhofoplosser in Java
1. Inleiding
In dit artikel zullen we mogelijke manieren onderzoeken om met Java door een doolhof te navigeren.
Beschouw het doolhof als een zwart-witafbeelding, met zwarte pixels voor muren en witte pixels voor een pad. Twee witte pixels zijn bijzonder: de ene is de ingang van het doolhof en de andere uitgang.
Gezien zo'n doolhof willen we een pad vinden van ingang naar uitgang.
2. Modelleren van het doolhof
We beschouwen het doolhof als een 2D-array met gehele getallen. De betekenis van numerieke waarden in de array is volgens de volgende conventie:
- 0 -> Weg
- 1 -> Muur
- 2 -> Doolhof binnenkomst
- 3 -> Doolhofuitgang
- 4 -> Celgedeelte van het pad van binnenkomst tot vertrek
We modelleren het doolhof als een grafiek. In- en uitgang zijn de twee speciale knooppunten waartussen het pad moet worden bepaald.
Een typische grafiek heeft twee eigenschappen: knooppunten en randen. Een rand bepaalt de connectiviteit van de graaf en verbindt het ene knooppunt met het andere.
Daarom gaan we uit van vier impliciete randen van elk knooppunt, die het gegeven knooppunt verbinden met zijn linker-, rechter-, bovenste en onderste knooppunt.
Laten we de handtekening van de methode definiëren:
openbare lijst oplossen (doolhof) {}De invoer voor de methode is een doolhof, die de 2D-array bevat, met de hierboven gedefinieerde naamgevingsconventie.
Het antwoord van de methode is een lijst met knooppunten, die een pad vormt van het entry-knooppunt naar het exit-knooppunt.
3. Recursieve Backtracker (DFS)
3.1. Algoritme
Een vrij voor de hand liggende benadering is om alle mogelijke paden te verkennen, die uiteindelijk een pad zullen vinden als dat bestaat. Maar een dergelijke benadering heeft een exponentiële complexiteit en zal niet goed opschalen.
Het is echter mogelijk om de hierboven genoemde brute force-oplossing aan te passen door bezochte knooppunten terug te volgen en te markeren om binnen een redelijke tijd een pad te verkrijgen. Dit algoritme wordt ook wel Diepte-eerst zoeken genoemd.
Dit algoritme kan worden beschreven als:
- Als we bij de muur zijn of een al bezocht knooppunt, retourneer mislukking
- Anders, als we het exit-knooppunt zijn, retourneer dan succes
- Anders voegt u het knooppunt toe aan de padlijst en reist u recursief in alle vier de richtingen. Als een fout wordt geretourneerd, verwijdert u het knooppunt uit het pad en retourneert u de fout. Padlijst bevat een uniek pad wanneer exit wordt gevonden
Laten we dit algoritme toepassen op het doolhof dat wordt weergegeven in figuur 1 (a), waar S het startpunt is en E de uitgang.
Voor elk knooppunt doorlopen we elke richting in volgorde: rechts, onder, links, boven.
In 1 (b) verkennen we een pad en raken we de muur. Daarna gaan we terug totdat een knoop wordt gevonden die niet-muur buren heeft, en verkennen een ander pad zoals getoond in 1 (c).
We raken opnieuw de muur en herhalen het proces om uiteindelijk de uitgang te vinden, zoals weergegeven in 1 (d):




3.2. Implementatie
Laten we nu de Java-implementatie bekijken:
Eerst moeten we de vier richtingen definiëren. We kunnen dit definiëren in termen van coördinaten. Deze coördinaten zullen, wanneer ze worden toegevoegd aan een bepaalde coördinaat, een van de aangrenzende coördinaten retourneren:
privé statische int [] [] DIRECTIONS = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}}; We hebben ook een hulpprogramma-methode nodig die twee coördinaten toevoegt:
private Coordinate getNextCoordinate (int row, int col, int i, int j) {return new Coordinate (row + i, col + j); }We kunnen nu de handtekening van de methode definiëren oplossen.De logica hier is eenvoudig - als er een pad is van entry naar exit, retourneer dan het pad, anders retourneer je een lege lijst:
openbare lijst oplossen (doolhof doolhof) {lijstpad = nieuwe ArrayList (); if (verken (doolhof, maze.getEntry (). getX (), maze.getEntry (). getY (), pad)) {retourpad; } return Collections.emptyList (); }Laten we de verkennen methode waarnaar hierboven wordt verwezen. Als er een pad is, retourneer dan true, met de lijst met coördinaten in het argument pad. Deze methode heeft drie hoofdblokken.
Ten eerste verwijderen we ongeldige knooppunten, d.w.z. de knooppunten die zich buiten het doolhof bevinden of deel uitmaken van de muur. Daarna markeren we het huidige knooppunt als bezocht, zodat we niet steeds hetzelfde knooppunt bezoeken.
Ten slotte bewegen we recursief in alle richtingen als de uitgang niet wordt gevonden:
private boolean Explore (Maze maze, int row, int col, List path) {if (! maze.isValidLocation (row, col) || maze.isWall (row, col) || maze.isExplored (row, col)) { teruggeven false; } path.add (nieuwe coördinaat (rij, kolom)); maze.setVisited (row, col, true); if (maze.isExit (row, col)) {return true; } for (int [] direction: DIRECTIONS) {Coordinate coordinate = getNextCoordinate (row, col, direction [0], direction [1]); if (verken (doolhof, coordinate.getX (), coordinate.getY (), pad)) {return true; }} path.remove (path.size () - 1); teruggeven false; }Deze oplossing gebruikt stapelgrootte tot de grootte van het doolhof.
4. Variant - Kortste pad (BFS)
4.1. Algoritme
Het hierboven beschreven recursieve algoritme vindt het pad, maar het is niet noodzakelijk het kortste pad. Om het kortste pad te vinden, kunnen we een andere benadering van het doorlopen van grafieken gebruiken die bekend staat als Breedte-eerst zoeken.
Bij DFS werden eerst een kind en al zijn kleinkinderen onderzocht, voordat ze doorgingen naar een ander kind. Terwijl we in BFS alle directe kinderen onderzoeken voordat we naar de kleinkinderen gaan. Dit zorgt ervoor dat alle knooppunten op een bepaalde afstand van het bovenliggende knooppunt tegelijkertijd worden verkend.
Het algoritme kan als volgt worden beschreven:
- Voeg het startknooppunt toe aan de wachtrij
- Terwijl de wachtrij niet leeg is, popt u een knooppunt en doet u het volgende:
- Als we de muur bereiken of het knooppunt is al bezocht, ga dan verder met de volgende iteratie
- Als het exitknooppunt is bereikt, ga dan terug van het huidige knooppunt naar het startknooppunt om het kortste pad te vinden
- Voeg anders alle directe buren in de vier richtingen in de wachtrij toe
Een belangrijk ding hier is dat de knooppunten hun ouder moeten bijhouden, d.w.z. van waar ze aan de wachtrij zijn toegevoegd. Dit is belangrijk om het pad te vinden zodra het exit-knooppunt is aangetroffen.
De volgende animatie toont alle stappen bij het verkennen van een doolhof met behulp van dit algoritme. We kunnen zien dat alle knooppunten op dezelfde afstand eerst worden verkend voordat we naar het volgende niveau gaan:

4.2. Implementatie
Laten we dit algoritme nu in Java implementeren. We zullen het ROUTEBESCHRIJVING variabele gedefinieerd in de vorige sectie.
Laten we eerst een hulpprogramma-methode definiëren om terug te gaan van een gegeven knoop naar zijn root. Dit wordt gebruikt om het pad te traceren zodra de uitgang is gevonden:
private List backtrackPath (Coordinate cur) {List path = new ArrayList (); Coördinaten iter = cur; while (iter! = null) {path.add (iter); iter = iter.parent; } terugweg; }Laten we nu de kernmethode definiëren oplossen. We zullen de drie blokken die worden gebruikt bij de DFS-implementatie hergebruiken, d.w.z. knooppunt valideren, bezochte knoop markeren en aangrenzende knooppunten doorkruisen.
We zullen slechts een kleine wijziging aanbrengen. In plaats van recursieve traversal gebruiken we een FIFO-datastructuur om buren te volgen en deze te herhalen:
openbare lijst oplossen (doolhof doolhof) {LinkedList nextToVisit = nieuwe LinkedList (); Coördinaat start = maze.getEntry (); nextToVisit.add (start); while (! nextToVisit.isEmpty ()) {Coördinaat cur = nextToVisit.remove (); if (! maze.isValidLocation (cur.getX (), cur.getY ()) || maze.isExplored (cur.getX (), cur.getY ())) {ga verder; } if (maze.isWall (cur.getX (), cur.getY ())) {maze.setVisited (cur.getX (), cur.getY (), true); doorgaan met; } if (maze.isExit (cur.getX (), cur.getY ())) {return backtrackPath (cur); } for (int [] direction: DIRECTIONS) {Coördinaat coördinaat = nieuwe coördinaat (cur.getX () + richting [0], cur.getY () + richting [1], cur); nextToVisit.add (coördinaat); maze.setVisited (cur.getX (), cur.getY (), true); }} return Collections.emptyList (); }5. Conclusie
In deze tutorial hebben we twee belangrijke grafische algoritmen beschreven: Diepte-eerst zoeken en Breedte-eerst zoeken om een doolhof op te lossen. We hebben ook besproken hoe BFS het kortste pad geeft van de ingang naar de uitgang.
Zoek voor meer informatie andere methoden op om een doolhof op te lossen, zoals het A * - en Dijkstra-algoritme.
Zoals altijd is de volledige code te vinden op GitHub.