Voorbeeld van een algoritme voor heuvelklimmen in Java
1. Overzicht
In deze tutorial laten we het Hill-Climbing-algoritme en de implementatie ervan zien. We zullen ook kijken naar de voordelen en tekortkomingen. Laten we, voordat we er direct op ingaan, de benadering van het genereren en testen van algoritmen kort bespreken.
2. Algoritme genereren en testen
Het is een heel eenvoudige techniek waarmee we het vinden van oplossingen kunnen algoritmen:
- Definieer de huidige staat als een begintoestand
- Pas elke mogelijke bewerking toe op de huidige staat en genereer een mogelijke oplossing
- Vergelijk de nieuw gegenereerde oplossing met de doelstatus
- Als het doel is bereikt of als er geen nieuwe staten kunnen worden gemaakt, stop dan. Ga anders terug naar stap 2
Het werkt erg goed bij eenvoudige problemen. Omdat het een uitputtende zoektocht is, is het niet haalbaar om er rekening mee te houden bij het omgaan met grote probleemruimten. Het is ook bekend als het British Museum-algoritme (probeert een artefact in het British Museum te vinden door het willekeurig te verkennen).
Het is ook het belangrijkste idee achter de Hill-Climbing Attack in de wereld van biometrie. Deze benadering kan worden gebruikt voor het genereren van synthetische biometrische gegevens.
3. Inleiding tot het eenvoudige algoritme voor heuvelklimmen
In de Hill-Climbing-techniek, beginnend aan de voet van een heuvel, lopen we omhoog tot we de top van de heuvel bereiken. Met andere woorden, we beginnen met de initiële status en we blijven de oplossing verbeteren totdat deze optimaal is.
Het is een variatie op een genereren-en-test-algoritme dat alle toestanden weggooit die er niet veelbelovend uitzien of die ons waarschijnlijk niet naar de doeltoestand zullen leiden. Om dergelijke beslissingen te nemen, maakt het gebruik van heuristieken (een evaluatiefunctie) die aangeeft hoe dicht de huidige status bij de doeltoestand is.
In eenvoudige bewoordingen, Hill-Climbing = genereren-en-testen + heuristieken
Laten we eens kijken naar het Simple Hill-klimalgoritme:
- Definieer de huidige staat als een begintoestand
- Loop totdat de doelstatus is bereikt of er geen operators meer kunnen worden toegepast op de huidige status:
- Pas een bewerking toe op de huidige staat en een nieuwe staat krijgen
- Vergelijken de nieuwe staat met het doel
- Afsluiten als de doeltoestand is bereikt
- Evalueer nieuwe toestand met heuristische functie en vergelijk het met de huidige staat
- Als de nieuwere staat dichterbij is naar het doel vergeleken met de huidige staat, update de huidige status
Zoals we kunnen zien, bereikt het de doelstatus met iteratieve verbeteringen. In het Hill-Climbing-algoritme is het vinden van een doel gelijk aan het bereiken van de top van de heuvel.
4. Voorbeeld
Hill Climbing Algorithm kan worden gecategoriseerd als een geïnformeerde zoekopdracht. We kunnen dus elke op een knooppunt gebaseerde zoekopdracht of problemen zoals het n-queens-probleem implementeren. Om het concept gemakkelijk te begrijpen, zullen we een heel eenvoudig voorbeeld nemen.
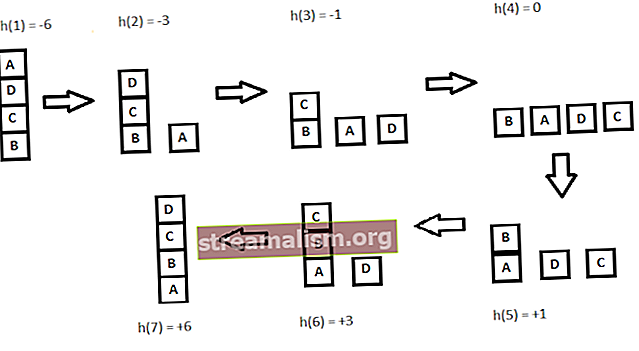
Laten we naar de onderstaande afbeelding kijken:

Het belangrijkste punt bij het oplossen van een probleem met het beklimmen van een heuvel is het kiezen van een geschikte heuristische functie.
Laten we een dergelijke functie definiëren u:
h (x) = +1 voor alle blokken in de draagconstructie als het blok correct gepositioneerd is, anders -1 voor alle blokken in de draagconstructie.
Hier noemen we elk blok correct gepositioneerd als het dezelfde ondersteuningsstructuur heeft als de doelstatus. Laten we, volgens de eerder besproken procedure voor heuvelklimmen, alle iteraties en hun heuristieken bekijken om de doeltoestand te bereiken:
 5. Implementatie
5. Implementatie
Laten we nu hetzelfde voorbeeld implementeren met behulp van het Hill-Climbing-algoritme.
Allereerst hebben we een Staat klasse die de lijst met stapels zal opslaan die posities van blokken in elke staat vertegenwoordigen. Het zal ook heuristieken voor die specifieke staat opslaan:
openbare klasse Staat {privélijst staat; private int heuristieken; // kopieer constructor, setters en getters} We hebben ook een methode nodig die de heuristische waarde van de staat berekent.
public int getHeuristicsValue (List currentState, Stack goalStateStack) {Integer heuristicValue; heuristicValue = currentState.stream () .mapToInt (stack -> {retour getHeuristicsValueForStack (stack, currentState, goalStateStack);}). sum (); terugkeer heuristicValue; } public int getHeuristicsValueForStack (Stack stack, List currentState, Stack goalStateStack) {int stackHeuristics = 0; boolean isPositioneCorrect = true; int goalStartIndex = 0; for (String currentBlock: stack) {if (isPositioneCorrect && currentBlock.equals (goalStateStack.get (goalStartIndex))) {stackHeuristics + = goalStartIndex; } anders {stackHeuristics - = goalStartIndex; isPositioneCorrect = false; } goalStartIndex ++; } return stackHeuristics; } Bovendien moeten we operatormethoden definiëren die ons een nieuwe status zullen geven. Voor ons voorbeeld zullen we twee van deze methoden definiëren:
- Knal een blok van een stapel en duw het op een nieuwe stapel
- Knal een blok van een stapel en duw het in een van de andere stapels
private State pushElementToNewStack (lijst currentStackList, String-blok, int currentStateHeuristics, Stack goalStateStack) {State newState = null; Stack newStack = new Stack (); newStack.push (blok); currentStackList.add (newStack); int newStateHeuristics = getHeuristicsValue (currentStackList, goalStateStack); if (newStateHeuristics> currentStateHeuristics) {newState = nieuwe staat (currentStackList, newStateHeuristics); } else {currentStackList.remove (newStack); } return newState; } private State pushElementToExistingStacks (Stack currentStack, List currentStackList, String block, int currentStateHeuristics, Stack goalStateStack) {return currentStackList.stream () .filter (stack -> stack! = currentStack) .map (stack -> {return pushElementToStack (stack, block, currentStackList, currentStateHeuristics, goalStateStack); }) .filter (Objects :: nonNull) .findFirst () .orElse (null); } private State pushElementToStack (Stack stack, String block, List currentStackList, int currentStateHeuristics, Stack goalStateStack) {stack.push (blok); int newStateHeuristics = getHeuristicsValue (currentStackList, goalStateStack); if (newStateHeuristics> currentStateHeuristics) {retourneer nieuwe staat (currentStackList, newStateHeuristics); } stack.pop (); null teruggeven; } Nu we onze hulpmethoden hebben, gaan we een methode schrijven om de techniek voor heuvelklimmen te implementeren.
Hier, we blijven nieuwe toestanden berekenen die dichter bij de doelen liggen dan hun voorgangers. We blijven ze op ons pad toevoegen totdat we het doel bereiken.
Als we geen nieuwe toestanden vinden, eindigt het algoritme met een foutmelding:
openbare lijst getRouteWithHillClimbing (Stack initStateStack, Stack goalStateStack) gooit uitzondering {// instantiate initState met initStateStack // ... List resultPath = new ArrayList (); resultPath.add (nieuwe staat (initState)); Staat currentState = initState; boolean noStateFound = false; while (! currentState.getState (). get (0) .equals (goalStateStack) || noStateFound) {noStateFound = true; Staat nextState = findNextState (currentState, goalStateStack); if (nextState! = null) {noStateFound = false; currentState = nextState; resultPath.add (nieuwe staat (nextState)); }} return resultPath; }Daarnaast hebben we ook nodig findNextState methode die alle mogelijke bewerkingen op de huidige status toepast om de volgende status te krijgen:
public State findNextState (State currentState, Stack goalStateStack) {List listOfStacks = currentState.getState (); int currentStateHeuristics = currentState.getHeuristics (); return listOfStacks.stream () .map (stack -> {return applyOperationsOnState (listOfStacks, stack, currentStateHeuristics, goalStateStack);}) .filter (Objects :: nonNull) .findFirst () .orElse (null); } public State applyOperationsOnState (List listOfStacks, Stack stack, int currentStateHeuristics, Stack goalStateStack) {State tempState; Lijst tempStackList = nieuwe ArrayList (listOfStacks); String block = stack.pop (); if (stack.size () == 0) tempStackList.remove (stack); tempState = pushElementToNewStack (tempStackList, block, currentStateHeuristics, goalStateStack); if (tempState == null) {tempState = pushElementToExistingStacks (stack, tempStackList, block, currentStateHeuristics, goalStateStack); stack.push (blok); } retourneer tempState; } 6. Steilste klimalgoritme voor heuvels
Het Steepest-Ascent Hill-Climbing-algoritme (gradiënt zoeken) is een variant van het Hill Climbing-algoritme. We kunnen het implementeren met kleine aanpassingen in ons eenvoudige algoritme. In dit algoritme, we overweeg alle mogelijke staten van de huidige staat en dan kies de beste als opvolger, in tegenstelling tot de eenvoudige heuvelklimtechniek.
Met andere woorden, in het geval van de heuvelklimtechniek hebben we elke staat als opvolger gekozen die dichter bij het doel lag dan de huidige staat, terwijl we in het Steepest-Ascent Hill Climbing-algoritme de beste opvolger uit alle mogelijke opvolgers kiezen en vervolgens updaten de huidige staat.
7. Nadelen
Hill Climbing is een kortzichtige techniek omdat het alleen onmiddellijke mogelijkheden evalueert. Het kan dus in enkele situaties terechtkomen waaruit het geen verdere staten kan kiezen. Laten we eens kijken naar deze staten en enkele oplossingen ervoor:
- Lokaal maximum: Het is een staat die beter is dan alle buren, maar er bestaat een betere staat die ver verwijderd is van de huidige staat; als het lokale maximum zich voordoet in het zicht van de oplossing, staat dit bekend als 'uitlopers'
- Plateau: In deze staat hebben alle aangrenzende staten dezelfde heuristische waarden, dus het is onduidelijk om de volgende staat te kiezen door lokale vergelijkingen te maken
- Nok: Het is een gebied dat hoger is dan de omringende staten, maar het kan niet in één beweging worden bereikt; We hebben bijvoorbeeld vier mogelijke richtingen om te verkennen (N, O, W, S) en er bestaat een gebied in NO-richting
Er zijn enkele oplossingen om deze situaties te verhelpen:
- Wij kunnen backtrack naar een van de vorige staten en verken andere richtingen
- We kunnen enkele staten overslaan en een springen in nieuwe richtingen
- Wij kunnen verken verschillende richtingen om het juiste pad te vinden
8. Conclusie
Hoewel heuvelklimtechniek veel beter is dan grondig zoeken, is het nog steeds niet optimaal in grote probleemruimtes.
We kunnen globale informatie altijd coderen in heuristische functies om slimmere beslissingen te nemen, maar dan zal de computationele complexiteit veel hoger zijn dan voorheen.
Het algoritme voor heuvelklimmen kan zeer nuttig zijn wanneer het met andere technieken wordt geknuppeld. Zoals altijd is de volledige code voor alle voorbeelden te vinden op GitHub.

 5. Implementatie
5. Implementatie