streamalism.org

1. Inleiding

In deze tutorial leren we over het algoritme voor gesimuleerd gloeien en laten we de voorbeeldimplementatie zien op basis van het Travelling Salesman Problem (TSP).

2. Gesimuleerd gloeien

Het Simulated Annealing-algoritme is een heuristiek voor het oplossen van de problemen met een grote zoekruimte.

De inspiratie en de naam kwamen van gloeien in de metallurgie; het is een techniek waarbij een materiaal wordt verwarmd en gecontroleerd.

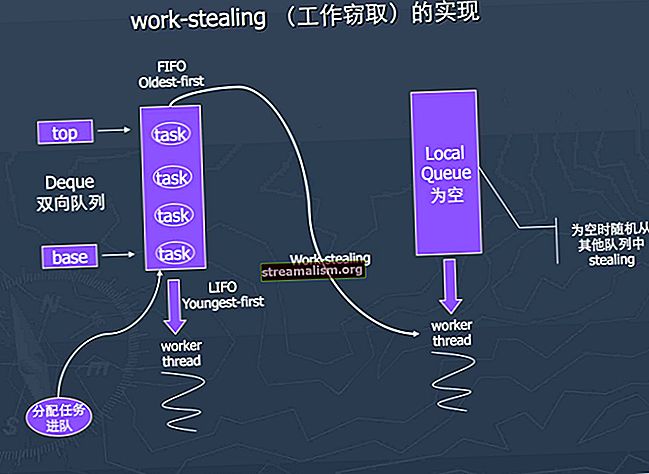
Over het algemeen vermindert de gesimuleerde gloeiing de kans op het accepteren van slechtere oplossingen, aangezien het de oplossingsruimte verkent en de temperatuur van het systeem verlaagt. De volgende animatie toont het mechanisme om de beste oplossing te vinden met het algoritme voor gesimuleerd gloeien:

Zoals we kunnen zien, gebruikt het algoritme een breder oplossingsbereik met hoge temperatuur van het systeem, op zoek naar een globaal optimum. Terwijl de temperatuur wordt verlaagd, wordt het zoekbereik kleiner, totdat het het globale optimum vindt.

Het algoritme heeft een paar parameters om mee te werken:

• aantal iteraties - stopconditie voor simulaties
• begintemperatuur - de startenergie van het systeem
• koelsnelheidparameter - het percentage waarmee we de temperatuur van het systeem verlagen
• minimumtemperatuur - optionele stopconditie
• simulatietijd - optionele stopconditie

De waarden van die parameters moeten zorgvuldig worden geselecteerd, aangezien ze een aanzienlijke invloed kunnen hebben op de prestaties van het proces.

3. Handelsreizigersprobleem

The Travelling Salesman Problem (TSP) is het bekendste optimalisatieprobleem op het gebied van informatica in een moderne wereld.

In eenvoudige bewoordingen is het een probleem om de optimale route tussen knooppunten in de grafiek te vinden. De totale reisafstand kan een van de optimalisatiecriteria zijn. Kijk hier voor meer informatie over TSP.

4. Java-model

Om het TSP-probleem op te lossen, hebben we twee modelklassen nodig, namelijk stad en Reizen. In de eerste slaan we de coördinaten van de knooppunten op in de grafiek:

@Data openbare klasse Stad {privé int x; privé int y; openbare stad () {this.x = (int) (Math.random () * 500); this.y = (int) (Math.random () * 500); } openbare dubbele afstandToCity (City city) {int x = Math.abs (getX () - city.getX ()); int y = Math.abs (getY () - city.getY ()); retourneer Math.sqrt (Math.pow (x, 2) + Math.pow (y, 2)); }}

De constructeur van stad class stelt ons in staat om willekeurige locaties van de steden te creëren. De distanceToCity (..) logic is verantwoordelijk voor berekeningen met betrekking tot de afstand tussen de steden.

De volgende code is verantwoordelijk voor het modelleren van een rondreis door een handelsreiziger. Laten we beginnen met het genereren van de eerste volgorde van steden in reizen:

public void generationInitialTravel () {if (travel.isEmpty ()) new Travel (10); Collections.shuffle (reizen); }

Naast het genereren van de eerste volgorde, hebben we de methoden nodig om de twee willekeurige steden in de reisvolgorde om te wisselen. We zullen het gebruiken om te zoeken naar de betere oplossingen binnen het algoritme voor gesimuleerd gloeien:

openbare ongeldige swapCities () {int a = generationRandomIndex (); int b = GenereerRandomIndex (); previousTravel = reizen; Stad x = travel.get (a); Stad y = travel.get (b); travel.set (a, y); travel.set (b, x); }

Verder hebben we een methode nodig om het genereren van swap in de vorige stap ongedaan te maken als de nieuwe oplossing niet door ons algoritme wordt geaccepteerd:

openbare leegte revertSwap () {travel = previousTravel; }

De laatste methode die we willen behandelen, is de berekening van de totale reisafstand, die zal worden gebruikt als een optimalisatiecriterium:

openbare int getDistance () {int afstand = 0; for (int index = 0; index <travel.size (); index ++) {Stad starten = getCity (index); Stad bestemming; if (index + 1 <travel.size ()) {bestemming = getCity (index + 1); } else {bestemming = getCity (0); } afstand + = start.distanceToCity (bestemming); } retour afstand; }

Laten we ons nu concentreren op het grootste deel, de implementatie van het gesimuleerde gloei-algoritme.

5. Implementatie van gesimuleerde gloeiing

In de volgende Simulated Annealing-implementatie gaan we het TSP-probleem oplossen. Even een korte herinnering, het doel is om de kortste afstand te vinden om alle steden te reizen.

Om het proces te starten, moeten we drie hoofdparameters opgeven, namelijk begintemperatuur, numberOfIterations en coolingRate:

openbare dubbele simulatieAnnealing (dubbele starttemperatuur, int numberOfIterations, dubbele coolingRate) {dubbele t = starttemperatuur; reizen.generateInitialTravel (); double bestDistance = travel.getDistance (); Travel currentSolution = reizen; // ...}

Voordat de simulatie begint, genereren we een initiële (willekeurige) volgorde van steden en berekenen we de totale reisafstand. Omdat dit de eerste berekende afstand is, slaan we deze op binnen de beste afstand variabele, naast de huidige oplossing.

In de volgende stap starten we een hoofdsimulatielus:

for (int i = 0; i 0.1) {// ...} else {continue; }}

De lus duurt het aantal iteraties dat we hebben gespecificeerd. Bovendien hebben we een voorwaarde toegevoegd om de simulatie te stoppen als de temperatuur lager of gelijk is aan 0,1. Het zal ons in staat stellen om de tijd van simulaties te besparen, omdat bij lage temperaturen de optimalisatieverschillen bijna niet zichtbaar zijn.

Laten we eens kijken naar de belangrijkste logica van het algoritme voor gesimuleerd gloeien:

currentSolution.swapCities (); dubbele currentDistance = currentSolution.getDistance (); if (currentDistance <bestDistance) {bestDistance = currentDistance; } anders if (Math.exp ((bestDistance - currentDistance) / t) <Math.random ()) {currentSolution.revertSwap (); }

Bij elke simulatiestap wisselen we willekeurig twee steden in de reisvolgorde.

Verder berekenen we de currentDistance. Als het nieuw berekende currentDistance is lager dan beste afstand, we bewaren het als de beste.

Anders controleren we of de Boltzmann-functie van de kansverdeling lager is dan de willekeurig gekozen waarde in een bereik van 0-1. Zo ja, dan draaien we de ruil van de steden terug. Zo niet, dan behouden we de nieuwe volgorde van de steden, omdat het ons kan helpen de lokale minima te vermijden.

Ten slotte verlagen we in elke stap van de simulatie de temperatuur door te voorzien koeling

t * = coolingRate;

Na de simulatie retourneren we de beste oplossing die we hebben gevonden met gesimuleerd gloeien.

Let op de enkele tips voor het kiezen van de beste simulatieparameters:

• voor kleine oplossingsruimten is het beter om de starttemperatuur te verlagen en de afkoelsnelheid te verhogen, omdat dit de simulatietijd verkort, zonder kwaliteitsverlies
• Kies voor grotere oplossingsruimten de hogere starttemperatuur en een kleine afkoelsnelheid, aangezien er meer lokale minima zullen zijn
• geef altijd voldoende tijd om te simuleren van de hoge naar de lage temperatuur van het systeem

Vergeet niet wat tijd te besteden aan het afstemmen van het algoritme met de kleinere probleeminstantie, voordat u met de hoofdsimulaties begint, omdat dit de eindresultaten zal verbeteren. De afstemming van het algoritme voor gesimuleerd gloeien werd bijvoorbeeld in dit artikel getoond.

6. Conclusie

In deze korte tutorial hebben we kunnen leren over het gesimuleerde gloei-algoritme en we hebben het handelsreizigersprobleem opgelost. Dit laat hopelijk zien hoe handig dit eenvoudige algoritme is, wanneer het wordt toegepast op bepaalde soorten optimalisatieproblemen.

De volledige implementatie van dit artikel is te vinden op GitHub.