streamalism.org

1. Overzicht

In deze korte zelfstudie laten we zien hoe u de afstand tussen twee punten in Java kunt berekenen.

2. De wiskundige formule van de afstand

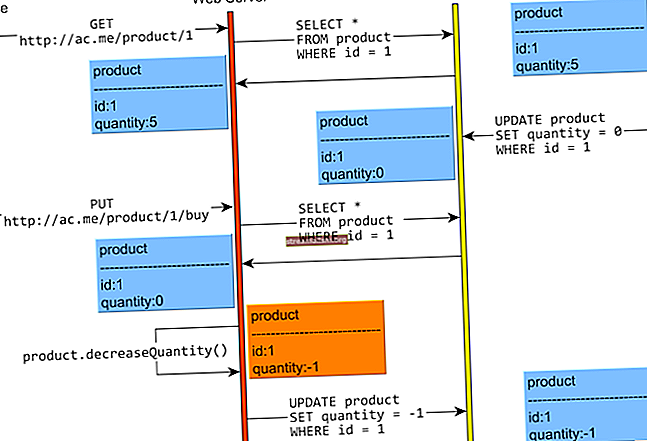
Stel dat we twee punten op een vlak hebben: het eerste punt A heeft de coördinaten (x1, y1) en het tweede punt B heeft de coördinaten (x2, y2). We willen AB berekenen, de afstand tussen de punten.

Laten we eerst een rechthoekige driehoek bouwen met de hypotenusa AB:

Volgens de stelling van Pythagoras is de som van de vierkanten van de lengtes van de benen van de driehoek hetzelfde als het kwadraat van de lengte van de hypotenusa van de driehoek: AB2 = AC2 + CB2.

Ten tweede, laten we AC en CB berekenen.

Duidelijk:

AC = y2 - y1

Evenzo:

BC = x2 - x1

Laten we de delen van de vergelijking vervangen:

afstand * afstand = (y2 - y1) * (y2 - y1) + (x2 - x1) * (x2 - x1)

Ten slotte kunnen we uit de bovenstaande vergelijking de afstand tussen de punten berekenen:

afstand = sqrt ((y2 - y1) * (y2 - y1) + (x2 - x1) * (x2 - x1))

Laten we nu verder gaan met het implementatiegedeelte.

3. Java-implementatie

3.1. Gebruik van gewone formule

Hoewel java.lang.Math en java.awt.geom.Point2D pakketten bieden kant-en-klare oplossingen, laten we eerst de bovenstaande formule implementeren zoals deze is:

openbare dubbele berekenDistanceBetweenPoints (dubbele x1, dubbele y1, dubbele x2, dubbele y2) {return Math.sqrt ((y2 - y1) * (y2 - y1) + (x2 - x1) * (x2 - x1)); }

Om de oplossing te testen, nemen we de driehoek met poten 3 en 4 (zoals weergegeven in de afbeelding hierboven). Het is duidelijk dat het nummer 5 is geschikt als de waarde van de hypotenusa:

3 * 3 + 4 * 4 = 5 * 5

Laten we de oplossing bekijken:

@ Test openbare ongeldig gegevenTwoPoints_whenCalculateDistanceByFormula_thenCorrect () {dubbele x1 = 3; dubbele y1 = 4; dubbel x2 = 7; dubbele y2 = 1; dubbele afstand = service.calculateDistanceBetweenPoints (x1, y1, x2, y2); assertEquals (afstand, 5, 0,001); }

3.2. Gebruik makend van java.lang.Math Pakket

Als het resultaat van vermenigvuldiging in de berekenDistanceBetweenPoints () methode is te groot, kan overstroming optreden. In tegenstelling tot dat, Math.hypot () methode voorkomt tussentijdse overloop of onderloop:

openbare dubbele berekenDistanceBetweenPointsWithHypot (dubbele x1, dubbele y1, dubbele x2, dubbele y2) {dubbele ac = Math.abs (y2 - y1); dubbele cb = Math.abs (x2 - x1); retourneer Math.hypot (ac, cb); }

Laten we dezelfde punten nemen als hiervoor en controleren of de afstand hetzelfde is:

@Test openbare ongeldig gegevenTwoPoints_whenCalculateDistanceWithHypot_thenCorrect () {dubbele x1 = 3; dubbele y1 = 4; dubbel x2 = 7; dubbele y2 = 1; dubbele afstand = service.calculateDistanceBetweenPointsWithHypot (x1, y1, x2, y2); assertEquals (afstand, 5, 0,001); }

3.3. Gebruik makend van java.awt.geom.Point2D Pakket

Laten we tot slot de afstand berekenen met de Point2D. Afstand () methode:

openbare dubbele berekenDistanceBetweenPointsWithPoint2D (dubbele x1, dubbele y1, dubbele x2, dubbele y2) {return Point2D.distance (x1, y1, x2, y2); }

Laten we nu de methode op dezelfde manier testen:

@Test openbare ongeldig gegevenTwoPoints_whenCalculateDistanceWithPoint2D_thenCorrect () {dubbele x1 = 3; dubbele y1 = 4; dubbel x2 = 7; dubbele y2 = 1; dubbele afstand = service.calculateDistanceBetweenPointsWithPoint2D (x1, y1, x2, y2); assertEquals (afstand, 5, 0,001); }

4. Conclusie

In deze zelfstudie hebben we een paar manieren getoond om de afstand tussen twee punten in Java te berekenen.

Zoals altijd is de code die in de voorbeelden wordt gebruikt, beschikbaar op GitHub.