streamalism.org

1. Inleiding

In deze tutorial we bespreken de oplossing van het k-combinaties probleem in Java.

Eerst bespreken en implementeren we zowel recursieve als iteratieve algoritmen om alle combinaties van een bepaalde grootte te genereren. Vervolgens zullen we oplossingen bekijken met behulp van algemene Java-bibliotheken.

2. Combinatiesoverzicht

Simpel gezegd, een combinatie is een subset van elementen uit een bepaalde set.

In tegenstelling tot permutaties, doet de volgorde waarin we de individuele elementen kiezen er niet toe. In plaats daarvan maakt het ons alleen uit of een bepaald element in de selectie zit.

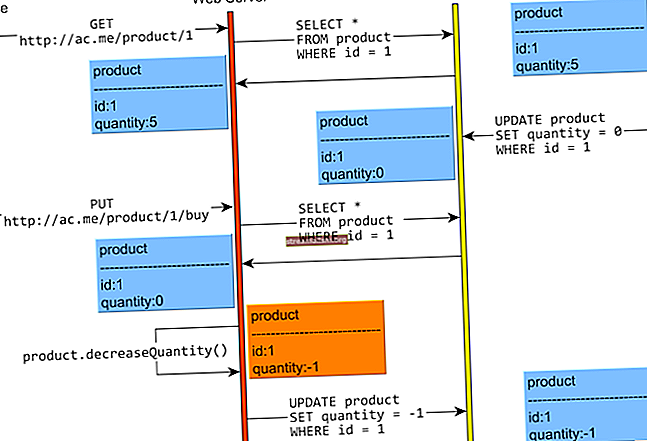
In een kaartspel moeten we bijvoorbeeld 5 kaarten delen uit het pakket bestaande uit 52 kaarten. We hebben geen interesse in de volgorde waarin de 5 kaarten zijn geselecteerd. Het maakt ons eerder alleen uit welke kaarten in de hand aanwezig zijn.

Bij sommige problemen moeten we alle mogelijke combinaties evalueren. Om dit te kunnen doen, zetten we de verschillende combinaties op een rij.

Het aantal verschillende manieren om 'r'-elementen uit de set van' n'-elementen te kiezen, kan wiskundig worden uitgedrukt met de volgende formule:

Daarom kan het aantal manieren om elementen te kiezen in het ergste geval exponentieel toenemen. Daarom is het voor grote populaties wellicht niet mogelijk om de verschillende selecties op te sommen.

In dergelijke gevallen kunnen we willekeurig enkele representatieve selecties selecteren. Het proces wordt aangeroepen bemonstering.

Vervolgens bekijken we de verschillende algoritmen om combinaties weer te geven.

3. Recursieve algoritmen om combinaties te genereren

Recursieve algoritmen werken meestal door een probleem op te delen in vergelijkbare kleinere problemen. Dit proces gaat door totdat we de eindconditie bereiken, die ook het basisscenario is. Dan lossen we het basisscenario direct op.

We bespreken twee manieren om de taak van het kiezen van elementen uit een set onder te verdelen. De eerste benadering verdeelt het probleem in termen van de elementen in de set. De tweede benadering verdeelt het probleem door alleen de geselecteerde elementen te volgen.

3.1. Partitioneren op basis van elementen in de hele set

Laten we de taak van het selecteren van "r ' elementen uit “n " items door de items een voor een te inspecteren. Voor elk item in de set kunnen we het in de selectie opnemen of uitsluiten.

Als we het eerste item opnemen, moeten we 'r – 1″ elementen uit de overige “n - 1 ″ items. Aan de andere kant, als we het eerste item weggooien, moeten we 'r ' elementen uit de resterende "n - 1 ″ items.

Dit kan wiskundig worden uitgedrukt als:

Laten we nu eens kijken naar de recursieve implementatie van deze aanpak:

private void helper (lijstcombinaties, int data [], int start, int end, int index) {if (index == data.length) {int [] combinatie = data.clone (); combinaties.add (combinatie); } else if (start <= end) {data [index] = start; helper (combinaties, data, begin + 1, einde, index + 1); helper (combinaties, data, begin + 1, einde, index); }}

De helper methode maakt twee recursieve aanroepen naar zichzelf. De eerste aanroep bevat het huidige element. De tweede aanroep verwijdert het huidige element.

Laten we vervolgens de combinatiegenerator hiermee schrijven helper methode:

openbare lijst genereren (int n, int r) {lijstcombinaties = nieuwe ArrayList (); helper (combinaties, nieuwe int [r], 0, n-1, 0); combinaties teruggeven; }

In de bovenstaande code, de genereren methode zet de eerste aanroep naar de helper methode en geeft de juiste parameters door.

Laten we vervolgens deze methode aanroepen om combinaties te genereren:

Lijstcombinaties = genereren (N, R); voor (int [] combinatie: combinaties) {System.out.println (Arrays.toString (combinatie)); } System.out.printf ("gegenereerde% d combinaties van% d items van% d", combined.size (), R, N);

Bij het uitvoeren van het programma krijgen we de volgende output:

[0, 1] [0, 2] [0, 3] [0, 4] [1, 2] [1, 3] [1, 4] [2, 3] [2, 4] [3, 4] genereerde 10 combinaties van 2 items van 5

Laten we tot slot de testcase schrijven:

@Test openbare ongeldige gegevenSetAndSelectionSize_whenCalculatedUsingSetRecursiveAlgorithm_thenExpectedCount () {SetRecursiveCombinationGenerator generator = nieuwe SetRecursiveCombinationGenerator (); Lijstselectie = generator.generate (N, R); assertEquals (nCr, selection.size ()); }

Het is gemakkelijk in te zien dat de vereiste stapelgrootte het aantal elementen in de set is. Als het aantal elementen in de set groot is, bijvoorbeeld groter dan de maximale aanroepstapeldiepte, lopen we over de stapel en krijgen we een StackOverflowError.

Daarom werkt deze benadering niet als de invoerset groot is.

3.2. Partitioneren op basis van elementen in de combinatie

In plaats van de elementen in de invoerset te volgen, we zullen de taak verdelen door de items in de selectie bij te houden.

Laten we eerst de items in de invoerset ordenen met behulp van de indexen "1" tot "n ". Nu kunnen we het eerste item uit het eerste kiezen "n-r + 1 ″ items.

Laten we aannemen dat we de kth item. Vervolgens moeten we kiezen "r - 1 ″ items van de resterende 'n - k " items geïndexeerd 'k + 1 ″ naar "n ".

We drukken dit proces wiskundig uit als:

De volgende, laten we de recursieve methode schrijven om deze aanpak te implementeren:

private void helper (lijstcombinaties, int data [], int start, int end, int index) {if (index == data.length) {int [] combinatie = data.clone (); combinaties.add (combinatie); } else {int max = Math.min (end, end + 1 - data.length + index); voor (int i = start; i <= max; i ++) {data [index] = i; helper (combinaties, data, i + 1, end, index + 1); }}}

In de bovenstaande code, de voor loop kiest het volgende item, dan, het noemt de helper() methode recursief om de resterende items te kiezen. We stoppen wanneer het vereiste aantal items is geselecteerd.

Laten we vervolgens de helper methode om selecties te genereren:

openbare lijst genereren (int n, int r) {lijstcombinaties = nieuwe ArrayList (); helper (combinaties, nieuwe int [r], 0, n - 1, 0); combinaties teruggeven; }

Laten we tot slot een testcase schrijven:

@Test openbare leegte gegevenSetAndSelectionSize_whenCalculatedUsingSelectionRecursiveAlgorithm_thenExpectedCount () {SelectionRecursiveCombinationGenerator generator = nieuwe SelectionRecursiveCombinationGenerator (); Lijstselectie = generator.generate (N, R); assertEquals (nCr, selection.size ()); }

De grootte van de call-stack die door deze benadering wordt gebruikt, is hetzelfde als het aantal elementen in de selectie. Daarom deze benadering kan werken voor grote inputs zolang het aantal te selecteren elementen kleiner is dan de maximale call stack-diepte.

Als het aantal te kiezen elementen ook groot is, zal deze methode niet werken.

4. Iteratief algoritme

Bij de iteratieve benadering beginnen we met een eerste combinatie. Dan, we blijven de volgende combinatie genereren van de huidige totdat we alle combinaties hebben gegenereerd.

Laten we de combinaties in lexicografische volgorde genereren. We beginnen met de laagste lexicografische combinatie.

Om de volgende combinatie van de huidige te krijgen, zoeken we de meest rechtse locatie in de huidige combinatie die kan worden verhoogd. Vervolgens verhogen we de locatie en genereren we de laagst mogelijke lexicografische combinatie rechts van die locatie.

Laten we de code schrijven die deze benadering volgt:

openbare lijst genereren (int n, int r) {lijstcombinaties = nieuwe ArrayList (); int [] combinatie = nieuwe int [r]; // initialiseren met de laagste lexicografische combinatie voor (int i = 0; i <r; i ++) {combinatie [i] = i; } while (combinatie [r - 1] <n) {combinaties.add (combinatie.clone ()); // genereer de volgende combinatie in lexicografische volgorde int t = r - 1; while (t! = 0 && combinatie [t] == ​​n - r + t) {t--; } combinatie [t] ++; voor (int i = t + 1; i <r; i ++) {combinatie [i] = combinatie [i - 1] + 1; }} retourcombinaties; }

Laten we vervolgens de testcase schrijven:

@Test openbare ongeldige gegevenSetAndSelectionSize_whenCalculatedUsingIterativeAlgorithm_thenExpectedCount () {IterativeCombinationGenerator generator = nieuwe IterativeCombinationGenerator (); Lijstselectie = generator.generate (N, R); assertEquals (nCr, selection.size ()); }

Laten we nu enkele Java-bibliotheken gebruiken om het probleem op te lossen.

5. Java-bibliotheken die combinaties implementeren

We moeten bestaande bibliotheekimplementaties zoveel mogelijk hergebruiken in plaats van onze eigen implementaties uit te rollen. In deze sectie zullen we de volgende Java-bibliotheken verkennen die combinaties implementeren:

• Apache Commons
• Guave
• CombinatoricsLib

5.1. Apache Commons

De CombinatoricsUtils class van Apache Commons biedt vele combinatiefuncties. In het bijzonder de combinatiesIterator methode retourneert een iterator die combinaties in lexicografische volgorde genereert.

Laten we eerst de Maven-afhankelijkheid toevoegen commons-math3 naar het project:

 org.apache.commons commons-math3 3.6.1 

De volgende, laten we de combinatiesIterator methode om de combinaties af te drukken:

openbare statische leegte genereren (int n, int r) {Iterator iterator = CombinatoricsUtils.combinationsIterator (n, r); while (iterator.hasNext ()) {final int [] combinatie = iterator.next (); System.out.println (Arrays.toString (combinatie)); }}

5.2. Google Guava

De Sets class uit de Guava-bibliotheek biedt hulpprogramma's voor setgerelateerde bewerkingen. De combinaties methode retourneert alle subsets van een bepaalde grootte.

Laten we eerst de maven-afhankelijkheid voor de Guava-bibliotheek aan het project toevoegen:

 com.google.guava guave 27.0.1-jre 

De volgende, laten we de combinaties methode om combinaties te genereren:

Set combinaties = Sets. combinaties (ImmutableSet.of (0, 1, 2, 3, 4, 5), 3);

Hier gebruiken we de Onveranderlijk methode om een ​​set te maken van de opgegeven nummers.

5.3. CombinatoricsLib

CombinatoricsLib is een kleine en eenvoudige Java-bibliotheek voor permutaties, combinaties, subsets, partities met gehele getallen en Cartesiaans product.

Om het in het project te gebruiken, voegen we het combinatoricslib3 Maven-afhankelijkheid:

 com.github.dpaukov combinatoricslib3 3.3.0 

De volgende, laten we de bibliotheek gebruiken om de combinaties af te drukken:

Generator.combination (0, 1, 2, 3, 4, 5) .simple (3) .stream () .forEach (System.out :: println);

Dit levert bij uitvoering de volgende uitvoer op:

[0, 1, 2] [0, 1, 3] [0, 1, 4] [0, 1, 5] [0, 2, 3] [0, 2, 4] [0, 2, 5] [0, 3, 4] [0, 3, 5] [0, 4, 5] [1, 2, 3] [1, 2, 4] [1, 2, 5] [1, 3, 4] [1, 3, 5] [1, 4, 5] [2, 3, 4] [2, 3, 5] [2, 4, 5] [3, 4, 5]

Meer voorbeelden zijn beschikbaar op combinatoricslib3-voorbeeld.

6. Conclusie

In dit artikel hebben we een aantal algoritmen geïmplementeerd om combinaties te genereren.

We hebben ook enkele bibliotheekimplementaties besproken. Meestal zouden we deze gebruiken in plaats van onze eigen te rollen.

Zoals gewoonlijk is de volledige broncode te vinden op GitHub.